Expression parsing algorithm
To evaluate a mathematical expression like 5-6/2+3*4, which is in the generally used form, a calculator first parses the expression into a form it can easily evaluate. Parsing is required because the order of operations matters. For example multiplication and division operations must be performed before addition and subtraction operations. The calculator relies on the precedence order of these operators (+ - * /) in order to determine what to compute first and what to compute next.
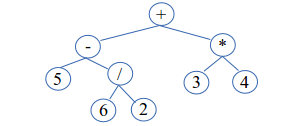
A simple way to represent a mathematical expression in a form that a calculator can easily evaluate is to represent it as a Binary Expression Tree. This is a data structure based on the concept of a node, represented by a circle containing an item (or value or ID), and which may have a left-child, right-child or parent node. A child node extends down its parent. Representing the expression 5-6/2+3*4 gives:
In order to evaluate this expression, a post-order traversal of the tree is done. That is, starting from the root node, child nodes are first evaluated recursively before their parent node is evaluated. Therefore the tree is evaluated starting from the bottom all the way up to the top. This gives:
(5-(6/2))+(3*4) = (5-3)+(3*4) = 2+12 = 14
This document presents a new, simple and very efficient iterative algorithm to parse a mathematical expression into a Binary Expression Tree. The expression is given in the generally used form also known as infix notation. For an expression of size n the performance is O(n), with a very small implementation constant. The algorithm is a type of operator-precedence parser. It was originally developed to parse the equation of a graph in the Graph Plotter 3D software.
Contents:
- The basic idea
- Using right associative operators
- Using the open and close brackets
- Using functions like sin() and cos()
- Using the negative and factorial operators
- Using the comparison and logical operators
- Analysis of performance and correctness
- Example implementation of the algorithm
- Parsing while evaluating with stack based algorithm
- Example implementation of stack based algorithm
- Links
- See also
The basic idea
The algorithm is given every item (operator or number) of the original expression one after another. It inserts each item directly into the tree. The basic idea lies in the insertion process and is based on the precedence ordering. The algorithm in its basic form is as follows:
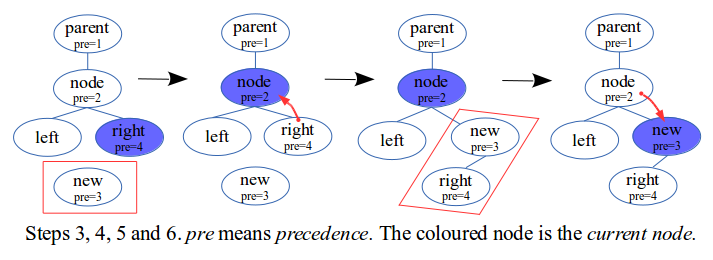
- Get the first item and initialise the tree with it.
- Currently the root node is also the current node. The current node is the node we currently lie on.
- Get the next item. This will be called the new item.
- Climb up the tree as long as the precedence of the current node item is greater than or equal to that of the new item. When this is over, the current node item has a precedence strictly less than that of the new item.
- Create a new node for the new item. Then set the left child of the new node to be the old right child of the current node. Finally set the new right child of the current node to be the new node (also set the parent of the new node).
- Set the current node to be the new node.
- Repeat steps 3, 4, 5 and 6 till there is no item left.
It can be observed that 1) we never move down the tree and 2) the current node is always on the right of its parent node. Notice that steps 4 and 5 form the basic idea behind the algorithm. In step 4, if at the root node then a node is imagined to hold the root node as its right child. Later we shall see that this imaginary node is in fact the open bracket node. In step 5 if there is nothing to set then nothing is set.
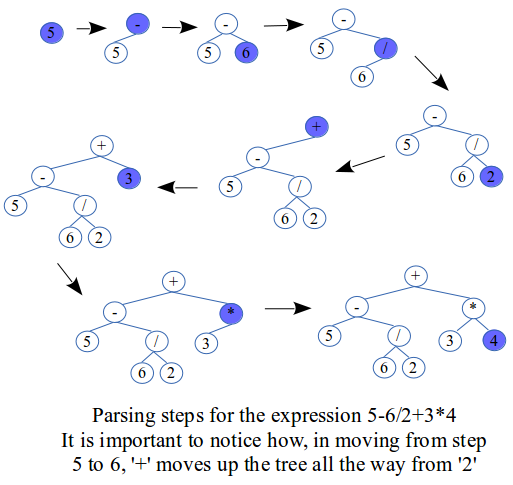
Now consider the following list of operators and their precedence levels:
- operator plus + with precedence 2
- operator minus - with precedence 2
- operator times * with precedence 4
- operator divide / with precedence 4
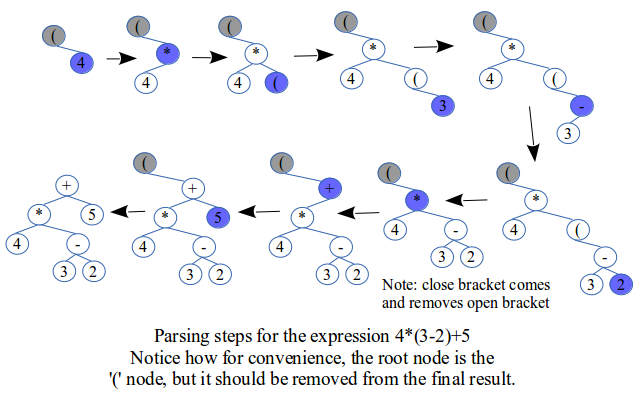
A number is given highest precedence. Below are the steps to parse the expression 5-6/2+3*4.
Using right associative operators
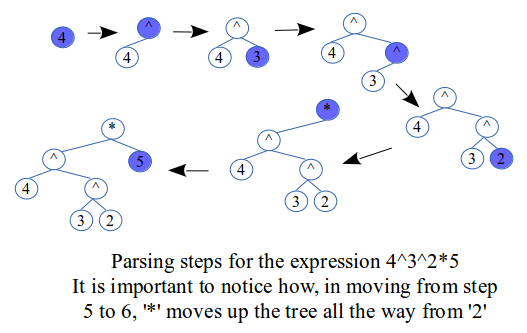
An example of a right associative operator is the exponent ^ operator. Lets add it to our list of operators and give it a precedence of 5. The 4 operators + - * / previously listed are left-associative. Step 4 is slightly changed to (everything else remains the same):
- Step 4: Climb up the tree as long as the precedence of the current node item is strictly greater than that of the new item. When this is over, the current node item has a precedence less than or equal to that of the new item.
Using the open and close brackets
The precedence levels of both '(' and ')' are set to 1, so they have the lowest precedence.
Using the open bracket:
This is inserted as if it had highest precedence. This essentially means skipping step 4 of the algorithm. The reason why '(' has the lowest precedence is so to avoid any other operator to get pass it while executing its step 4.
Using the close bracket:
First of all the slightly modified version of step 4 as used by right-associative operators is performed. The purpose is to climb up the tree and stop at the first encounter of an '(' node. Then what is done is simple: the '(' node is deleted. Essentially, steps 5 and 6 are changed to:
- Step 5: Set the new right child of the parent node to be the old right child of the current node, then delete the current node.
- Step 6: Set the current node to be the parent node.
There is no need to set the new parent of the right child node because we never move down the tree, but do set it so to maintain tree structure. Notice that the '(' node never has a left child.
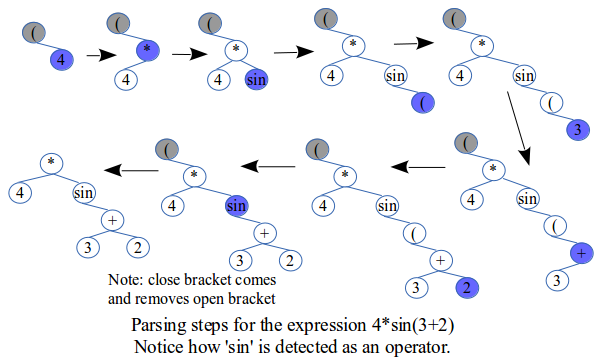
Using functions like sin() and cos()
This is based on the presence of the open and close brackets. Essentially, thinking about sin(3+2) is just like thinking about +(3+2) or *(3+2). The only differences are that the function name 'sin' is detected as an item, has only a right-operand, and has highest precedence just like a number.
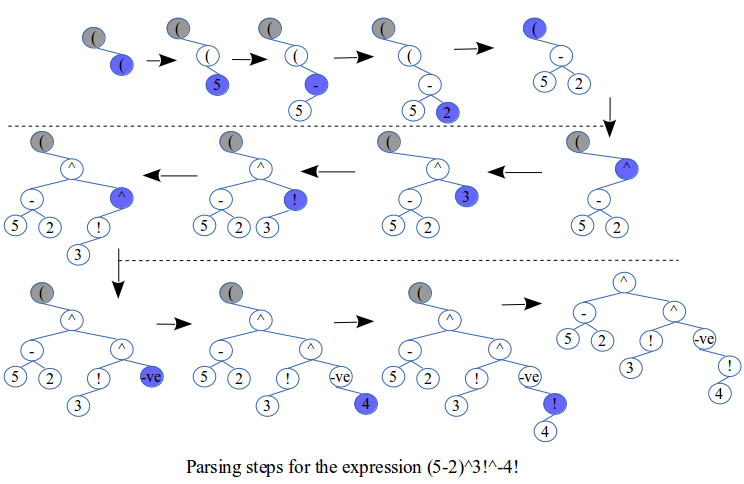
Using the negative and factorial operators
Lets add the negative '-ve' operator to our list of operators and give it a precedence of 3. Therefore it has a higher precedence than plus '+' and minus '-' but a lower precedence than times '*' and divide '/'. Also it has only a right-operand to operate on. For example in 4*-2 = 4*(-2), the operand '2' is negated. It is inserted in the same way as the open bracket: by skipping step 4.
Lets add the factorial '!' operator to our list of operators and give it a precedence of 6. Therefore it has a higher precedence than the exponent '^'. Also it has only a left-operand to operate on. For example in 4!*2 = (4!)*2, the factorial of the operand '4' is evaluated. It is inserted in the tree in the original basic way.
Our complete list of operators is now:
- operators ( and ) with precedence 1
- operator plus + with precedence 2
- operator minus - with precedence 2
- operator negative - with precedence 3
- operator times * with precedence 4
- operator divide / with precedence 4
- operator exponent ^ with precedence 5
- operator factorial ! with precedence 6
Functions and numbers have highest precedence.
Using the comparison and logical operators
Lets try to fit in the six comparison operators: equal ==, not equal !=, less than <, greater than >, less than or equal <=, and greater than or equal >=. Note that the precedence value is not really important; what is important is the precedence level. So lets give them all a precedence of 1.8, so they have higher precedence than '( )' and lower precedence than '+'.
Lets also try to fit in the following three logical operators into our list of operators:
- operator or with precedence 1.2
- operator and with precedence 1.4
- operator not with precedence 1.6
Notice that here the and operator is made to have higher precedence than the or operator.
The logical operators and and or are both associative. For example the expression (2==7 and 9==9 and 15==11) can be evaluated as ((2==7 and 9==9) and 15==11) or as (2==7 and (9==9 and 15==11)). The order does not matter. Therefore the algorithm as initially stated can be applied.
The logical operator not has only a right-operand to operate on. For example in the expression (9==9 and not 2==7) same as (9==9 and (not 2==7)), the result from 2==7, which is false, is negated to true. So the whole expression evaluates to (true and true) = true. This operator is inserted in the same way as the negative operator.
The comparison operators are non-associative. That is the expression (4==a==9) cannot be evaluated as ((4==a)==9) nor as (4==(a==9)). The reason is that 4==a evaluates to either true or false, but then the expression (true==9) is invalid. Actually what we will want is for the expression to evaluate as (4==a and a==9). Similarly we will want the expression (a<b<c<d) to evaluate as (a<b and b<c and c<d). This requires a more advanced tree structure.
Performance:
The performance analysis of the algorithm is very simple. The key is to note that we never move down the tree. Therefore every node is visited at most twice:
- On step 5 where the node is created and set.
- On step 4 when the node is passed by another climbing up.
Therefore the algorithm is given n items, creates n nodes for each of these and may visit a node again only once. This gives an algorithmic performance of O(2n). However step 5 involves a larger implementation constant than step 4.
Correctness:
The necessary and sufficient condition for the constructed binary expression tree to be valid is for it to respect the precedence orders of operations, which in turn will ensure proper order of evaluation of these operations. Therefore the algorithm is correct if it guarantees a valid constructed tree.
Respecting precedence orders implies that items with higher precedence levels must be found lower down the tree. Notice that this is exactly what step 4 of the algorithm ensures when it climbs up. Then step 5 follows by placing these items on a left sub-tree, never visited again since the current node is always on the right of its parent. With these two steps combined, it is guaranteed that a post-order traversal of the constructed tree will follow proper order of evaluation.
Some operators exhibit the important behaviour of skipping step 4 of the algorithm. This simply goes by the nature of the operators themselves. That is for the '(' and '-ve' operators for example, their first encounter implies highest precedence on insertion, which implies skipping step 4.
Example implementation of the algorithm
/*
To compile with GCC, execute:
gcc -Wall -ansi -pedantic -o calc expression-parsing-algorithm.c -lm
To run, execute: ./calc 1+1 5-6/2+3*4
*/
#include <stdio.h>
#include <string.h>
#include <malloc.h>
#include <math.h>
void* parse_expression (const char* expression);
double evaluate_expression_tree (const void* tree);
void print_expression_tree (const void* tree);
void delete_expression_tree (void* tree);
int main (int argc, char** argv)
{
void* tree;
double result;
int i;
if(argc<=1) printf("Usage: <program> <expression1> <expression2> ...\n");
for(i=1; i<argc; i++)
{
printf("________________________________%d_\n", i);
tree = parse_expression(argv[i]);
if(tree==NULL) continue;
print_expression_tree(tree);
result = evaluate_expression_tree(tree);
delete_expression_tree(tree);
printf("result = %f\n", result);
}
return 0;
}
/* ... rest of source code ... */
Download the complete C source code
Below is the portion of the source code that implements the algorithm.
typedef struct _Node {
enum NodeID ID;
int pre; /* precedence */
double number;
struct _Node *left, *right, *parent;
} Node;
Node* insert_node_item (Node* current, Node item, enum NodeInfo info)
{
Node* node;
if(info != SkipClimbUp)
{
/* step 4: climb up */
if(info != RightAssociative)
{
/* for left-associative */
while(current->pre >= item.pre)
current = current->parent;
}
else
{
/* for right-associative */
while(current->pre > item.pre)
current = current->parent;
}
}
if(item.ID == CLOSEBRACKET)
{
/* step 5.1: remove the '(' node */
node = current->parent;
node->right = current->right;
if(current->right) current->right->parent = node;
/* step 5.2: delete the '(' node */
memset(current, 0, sizeof(Node));
free(current);
/* step 6: Set the 'current node' to be the parent node */
current = node;
}
else
{
/* step 5.1: create the new node */
node = malloc(sizeof(Node));
*node = item;
node->right = NULL;
/* step 5.2: add the new node */
node->left = current->right;
if(current->right) current->right->parent = node;
current->right = node;
node->parent = current;
/* step 6: Set the 'current node' to be the new node */
current = node;
}
return current;
}
Parsing while evaluating with stack based algorithm
This is an optimally space-efficient algorithm that uses a simple stack array. Precisely, in the best case the space efficiency is O(1) and in the worst case it is O(n). Looking at the original algorithm which uses the binary expression tree, an important observation can be made which forms the basic idea behind the stack-based algorithm, which is that the left sub-tree can be evaluated during parsing.
It turns out that this stack-based version is essentially the Precedence Climbing algorithm, for the reason that it considers a binary tree structure. The tree-based version can however be designed with a more advanced tree structure, such as would be required to parse source code inside a compiler, such as is implemented in the Rhyscitlema computer application.
...to be updated...
As may be noticed from the source code below, this section is harder to explain...
Consider donating at https://www.rhyscitlema.com/donate to encourage improvement!
Example implementation of stack based algorithm
/*
To compile with GCC, execute:
gcc -Wall -ansi -pedantic -o calc expression-parse-and-evaluate.c -lm
To run, execute: ./calc 1+1 5-6/2+3*4
*/
#include <stdio.h>
#include <string.h>
#include <assert.h>
#include <math.h>
double parse_and_evaluate_expression (const char* expression);
int main (int argc, char** argv)
{
double result;
int i;
if(argc<=1) printf("Usage: <program> <expression1> <expression2> ...\n");
for(i=1; i<argc; i++)
{
printf("________________________________%d_\n", i);
result = parse_and_evaluate_expression(argv[i]);
printf("result = %f\n", result);
}
return 0;
}
/* ... rest of source code ... */
Download the complete C source code
Below is the portion of the source code that implements the algorithm.
typedef struct _Node {
enum NodeID ID;
int pre; /* precedence */
double number;
} Node;
Node* insert_node_item (Node* current, Node item, enum NodeInfo info)
{
double left, right;
if(info == SkipClimbUp) current+=1;
else
{
while(1)
{
if(info == RightAssociative)
{ if(current->pre <= item.pre) break; }
else { if(current->pre < item.pre) break; }
left = (current-1)->number;
right = (current+1)->number;
switch(current->ID)
{
case POSITIVE: ( current)->number = +right; break;
case NEGATIVE: ( current)->number = -right; break;
case PLUS: (--current)->number = left + right; break;
case MINUS: (--current)->number = left - right; break;
case TIMES: (--current)->number = left * right; break;
case DIVIDE: (--current)->number = left / right; break;
case EXPONENT: (--current)->number = pow(left, right); break;
case FACTORIAL: (--current)->number = factorial(left); break;
case SIN: ( current)->number = sin(right); break;
case COS: ( current)->number = cos(right); break;
case TAN: ( current)->number = tan(right); break;
default: break;
}
current->ID = NUMBER; /* force node to be a number */
current->pre = 10; /* set to highest precedence */
current--; /* prepare for next iteration */
}
switch(item.ID)
{
case CLOSEBRACKET:
*current = *(current+1);
/* current-=1; this part is optional */
break;
case PLUS:
case MINUS:
case TIMES:
case DIVIDE:
case EXPONENT:
case FACTORIAL: current+=2; break;
default: current+=1; break;
}
}
if(item.ID != CLOSEBRACKET)
*current = item;
return current;
}
Links
- http://en.wikipedia.org/wiki/Binary_expression_tree
- https://en.wikipedia.org/wiki/Tree_traversal
- https://en.wikipedia.org/wiki/Infix_notation
- https://en.wikipedia.org/wiki/Time_complexity#Linear_time
- http://en.wikipedia.org/wiki/Operator-precedence_parser
- https://github.com/rhyscitlema/librfet
See also