Strange generation of permutations

Permutations, when arranged in order can be numbered (or indexed or ranked) from 0 to n!-1, where n is the size of a permutation sequence. This article presents a new method of generating all permutations starting from a base permutation. The algorithm produces permutations such that a derived permutation follows its base permutation with differences in exactly two positions.

For example the permutation sequence {0, 1, 2, 3, 4} can be followed by {1, 0, 2, 3, 4} where both differ only in their values at the first and second positions. The algorithm is not really strange... just that it has not been named yet.

Contents:

  1. Ordered list of permutations
  2. Pattern in the ordered list
  3. Tree pre-order traversal
  4. Implementation of algorithm

Ordered list of permutations

This article strongly assumes that you have read that on generating permutations. Essentially we let I to be the index of (or rank of) a particular permutation. We let p to be the permutation sequence of the form {p0, p1, p2, ..., pn-2, pn-1}. plevel in this sequence is an integer between 0 and n-1 inclusive. It is found at a certain level (there are n levels from 0 to n-1).

Below is an example of numbered permutations in order for the case of n=4.
     index(I)  sequence(p)
        0    -   0 1 2 3
        1    -   1 0 2 3
        2    -   0 2 1 3
        3    -   2 0 1 3
        4    -   1 2 0 3
        5    -   2 1 0 3
        6    -   0 1 3 2
        7    -   1 0 3 2
        8    -   0 3 1 2
        9    -   3 0 1 2
        10   -   1 3 0 2
        11   -   3 1 0 2
        12   -   0 2 3 1
        13   -   2 0 3 1
        14   -   0 3 2 1
        15   -   3 0 2 1
        16   -   2 3 0 1
        17   -   3 2 0 1
        18   -   1 2 3 0
        19   -   2 1 3 0
        20   -   1 3 2 0
        21   -   3 1 2 0
        22   -   2 3 1 0
        23   -   3 2 1 0

Pattern in the ordered list

There is a certain pattern in the ordered list of permutations. The algorithm is all about understanding this pattern and then describing it using only the indexing variable I. Given an arbitrary value of I, which represents a particular permutation sequence p, the algorithm produces another value, say newI, such that its corresponding permutation sequence, say new_p, is different from p in exactly two positions.

There are two types of newI that are created, if they exist, from any given I and so there are two functions, say A and B. For every newI created it is recursively processed. The functions A and B call themselves recursively in a rather strange mixture. It is rather hard to understand what they are doing! Also they are still to be compressed into a single function.

Starting from the base permutation p={0, 1, 2, 3}, where I=0, the output is essentially: 
    cause  I   newI     p of newI
      A    0    1    -   1 0 2 3
      A    1    3    -   2 0 1 3
      A    3    9    -   3 0 1 2
      B    9    15   -   3 0 2 1
      B    15   21   -   3 1 2 0
      B    3    5    -   2 1 0 3
      A    5    11   -   3 1 0 2
      B    11   17   -   3 2 0 1
      B    17   23   -   3 2 1 0
      A    1    7    -   1 0 3 2
      B    7    13   -   2 0 3 1
      B    13   19   -   2 1 3 0
      A    0    2    -   0 2 1 3
      A    2    8    -   0 3 1 2
      B    8    14   -   0 3 2 1
      B    14   20   -   1 3 2 0
      B    2    4    -   1 2 0 3
      A    4    10   -   1 3 0 2
      B    10   16   -   2 3 0 1
      B    16   22   -   2 3 1 0
      A    0    6    -   0 1 3 2
      B    6    12   -   0 2 3 1
      B    12   18   -   1 2 3 0

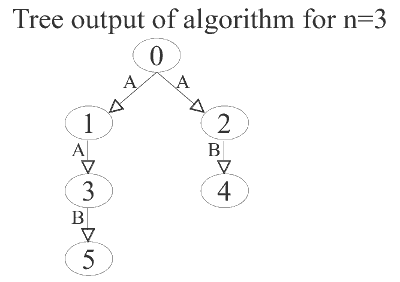
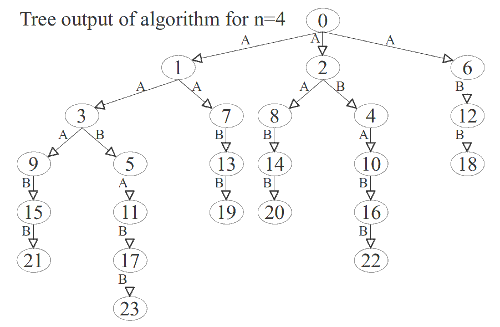
Tree pre-order traversal

It is better to understand what is going on using a pre-order traversal of a tree data structure that describes the running of the algorithm. In the example trees below a node is labeled with its value of I and an edge is labeled A or B. The edge label tells which function generates the newI value in the child node from the I value in the parent node.

To get the corresponding sequence p from a given value of I, go to generating permutations.




Implementation of algorithm

The source code below implements the algorithm. The program prints the tree structure, such that every line:
#include <stdio.h>

void function_A (int n, int I, int level);
void function_B (int n, int I, int level);
int factorial (int k);
void add (int process, int n, int I, int newI, int chr);

int tree[100000][20];
// the tree describes the running of the algorithm.
// a pre-order traversal of the tree corresponds
// to the permutations as printed on the screen.


int main()
{
	int n;
	printf("Enter n : ");   // get value of n
	scanf("%d", &n);

	printf("\n");
	add(0,0,0,0,0);         // initialise the tree

	function_A (n, 0, 1);   // run the algorithm

	add(2,n,0,0,0);         // print the tree

	return 0;
}


void function_A (int n, int I, int level)
{
	int i, newI;
	for(i=level; i<n; i++)
	{
		newI = I + factorial(i);
		add(1, n, I, newI, 'A');
		function_B (n, newI, i);
	}
}

void function_B (int n, int I, int level)
{
	function_A (n, I, level+1);

	int newI = I + factorial(level);
	if(newI >= factorial(level+1)) return; // base case

	add(1, n, I, newI, 'B');
	function_B (n, newI, level);
}


int factorial (int k)
{
	int i, ans=1;
	for(i=k; i>0; i--) ans*=i;
	return ans;
}

/* 
	The 'add' function below:
	- initialises the tree, when process==0
	- adds newI as a child to the node I, when process==1
	- prints the tree as an adjacency-list, when process==2
*/
void add (int process, int n, int I, int newI, int chr)
{
	int i, j;
	if(process==0)
	{
		for(i=0; i<10000; i++)
			tree[i][0]=0;
	}
	else if(process==1)
	{
		tree[I][0]++;
		tree[I][tree[I][0]*2] = newI;
		tree[I][tree[I][0]*2+1] = chr;
	}
	else if(process==2)
	{
		printf("Tree:\n");
		for(i=0; i<factorial(n); i++)
		{
			printf(" %d  %d  ", i, tree[i][0]);
			for(j=1; j<=tree[i][0]; j++)
				printf("  %d %c", tree[i][j*2], (char)tree[i][j*2+1]);
			printf("\n");
		}
	}
	else printf("process unknown\n");
}