Sorted List to complete BST
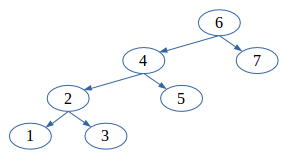
A sorted list (or sequence or array or linked-list) is a list that contains elements arranged in a sorted order. For example the sequence {1, 2, 3, 4, 5, 6, 7}. A binary search tree (BST) is a tree structure for which for every node, the left sub-tree has values less than that of the node and the right sub-tree has values greater than that of the node - typically. An example of a BST is:
An in-order traversal of a binary search tree generates a sorted list. That is, starting from the root node and in a recursive procedure, or starting from the left-most node and in an iterative procedure, the value of the left child node is first obtained, followed by that of the parent node, followed by that of the right child node. So for the BST above the sequence {1, 2, 3, 4, 5, 6, 7} is generated. Conversely, a binary search tree can be generated from a sorted list by an in-order construction of a binary tree. That is, as the sorted list is traversed from left to right, each element is used to create a new node which is then added to the binary tree in the exact same way as that node would have been visited under an in-order traversal.
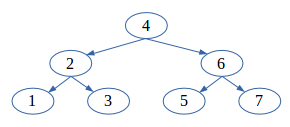
There are many forms in which the constructed tree can be. It can even be one without any left child node (the left-most node being the root node). However for optimal usefulness of the BST, all its levels must be full except at the leaves which may or may not be full. An example is the perfect binary tree below:
This article presents an iterative algorithm to perform an in-order construction of a complete binary tree. This is a binary tree for which all levels are full except maybe at the leaves which however are gathered on the left. The algorithm is based on the same basic principle as that used by the expression parsing algorithm, along with an added rule to ensure completeness. For a list of size n, the performance is O(n) and with very small implementation constant. The space complexity is O(log n log log n).
Contents:
- Constructing the binary tree
- Ensuring a complete binary tree
- Example implementation of the algorithm
- Links
- See also
Constructing the binary tree
The binary tree is constructed in a way that is similar to how the added nodes would have been visited nodes in an in-order traversal of the final tree. However this does not provide enough information to get started, as a binary tree can be in many different forms (like the two examples above). Information about which form the final tree must be in, is considered: the construction must ensure that leaves are at the same level. For a list of size n=2k-1, for example n=23-1=7, it implies that the constructed tree will be a perfect binary tree.
How to ensure that the leaves are at the same level? By observing the sequence {1, 2, 3, 4, 5, 6, 7} it is clear that 1 will be the left-most leave. In which case it is also clear that 2 will be one level higher than 1, and 3 will be the next leave. 2 will carry 1 and 3 as a perfect binary sub-tree. So 4 will have to carry 2 (as a left child) thereby being two levels higher than 1. Irrespective of the number of elements remaining, the left sub-tree of 4 is full. Whatever comes next will have to go to the right sub-tree until it is also full. So 5, 6 and 7 get added in the same way as 1, 2 and 3 but on the right of 4.
A general procedure is needed. The following observations are made:
- The first right child of any node is always a leave. This is very important for the next section. Node 1 is actually the first right child of an imaginary root node which carries the entire constructed tree.
- A perfect binary sub-tree has its root node carried by a node one level higher: 4 carries 2, 2 carries 1, and 1 carries the null node. Also the imaginary root carries 4 (it is at three levels higher than 1).
- The levels can be numbered: a null node is at level zero, a leave (such as 1) is at level one, 2 is at level two, 4 is at level three, the imaginary root is at level four (= 1+3 = 1 + the number of bits of n).
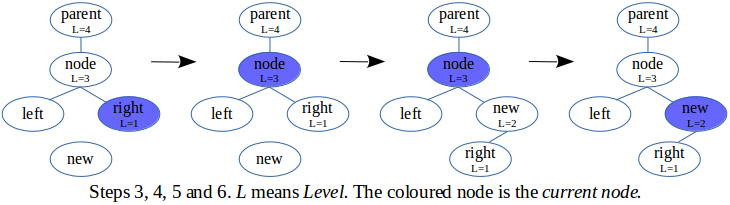
- During construction, when a sub-tree is full the algorithm climbs up the tree and stops when the difference in levels is greater than one, after which it inserts a new node.
The construction algorithm is given every element of the list one after another from beginning to end. It inserts each element directly into the tree. The basic idea lies in the insertion process. It is based on the level number of the binary tree levels. The algorithm is as follows:
- Create the imaginary root node, and set its level number to 1 + the number of bits of n.
- Currently the root node is also the current node. The current node is the node we currently lie on.
- Get the next element in the list and create a new node with it.
- Climb up the tree as long as the level number of the current node is one greater than that of its child node. This child is always the right child, since the current node is always on the right of its parent. No right child means a null node whose level number is zero.
- Set the level number of the new node to be one greater than that of the old right child. Then set the left child of the new node to be the old right child of the current node. Finally set the new right child of the current node to be the new node (also set the parent of the new node). If there is nothing to set then nothing is set.
- Set the 'current node' to be the new node.
- Repeat steps 3, 4, 5 and 6 till there is no element left.
Below are the steps to create a binary tree from the sequence {1, 2, 3, 4, 5, 6, 7}.
Ensuring a complete binary tree
The algorithm presented in the previous section will always produce a perfect binary tree for a list of size n=2k-1. But for a list size such as 4, it can be observed from the example presented that the tree may even not be balanced. Still the left sub-tree will always be a perfect binary sub-tree (since it starts off as a right sub-tree which gets full). For most applications this will probably be good enough.
In order to ensure that the constructed tree is a complete binary tree, two observations are first made about the original algorithm: the leaves are already gathered on the left, and the result will be a perfect tree if an appropriate number of nodes are still remaining to be added. The second observation is particularly important, as it is the principle behind the added rule that ensures a complete binary tree.
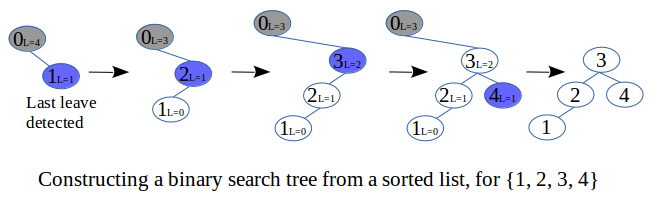
The rule is that: directly after all the leaves of the final tree have been added, the tree levels are all stepped down by one level. So an appropriate number of leaves then remains for the construction of a perfect binary tree (whose levels are one less than that of the final tree). The old second level (L=2) becomes the new leave level (L=1) and the old leave level becomes the new null level (L=0). If this happens when the current node is the last leave (as will typically be the case) then it is set to its parent (which is now at L=1).
The rule requires the number of leaves to be known before the algorithm starts. The number of leaves of a complete binary tree of size n is =
n+1 - 2h , where h = floor(log2(n+1))
The list may first be traversed once in order to get its size n.
Below are the steps to create a complete binary tree from the sequence {1, 2, 3, 4}.
Example implementation of the algorithm
The C source code below implements the final algorithm. A stack array is used to store the level numbers, instead of storing them inside the nodes. A stack structure is used because it describes best the behaviour of the current node as it moves up and down the tree during the construction. There are O(log n) levels and each requires O(log log n) space to be stored. Therefore the stack array has a total space complexity of O(log n log log n). This is small enough to be considered constant with respect to log(n).
#include <stdio.h>
#include <malloc.h>
typedef struct _Node
{
int data;
struct _Node *next; // for the Sorted Linked-List
struct _Node *parent, *left, *right; // for the BST
} Node;
void print_tree (const Node* node, int indent)
{
int i;
if(node==NULL) return;
print_tree (node->right, indent+4); // print right sub-tree
for(i=0; i<indent; i++) putchar(' '); // print indent spaces
printf("%d\r\n", node->data); // print current node
print_tree (node->left, indent+4); // print left sub-tree
}
Node* sorted_list_to_complete_binary_search_tree (Node* list)
{
int i, n; // needed storage size is k=log(n)
char h; // needed storage size is log(k)
char stack[32]; // needed storage size is k*log(k)
int leaves; // = number of leaves remaining
Node *current; // = pointer to current node
Node root = {0}; // = root node that holds the tree
if(list==NULL) return NULL;
// get the length 'n' of the list
for(n=0, current=list; current!=NULL; current = current->next, n++);
for(h=0, i=n+1; i>1; i=i>>1, h++); // get h = floor(log2(n+1))
leaves = n+1 - (1<<h); // get number of leaves = n+1 - 2^h
printf("n = %d , leaves = %d\r\n", n, leaves);
// prepare to start
if(leaves!=0) h++; // Get h = number of bits of n (by improvising!)
stack[0] = h+1; // Set initial content of stack: the root node
stack[1] = 0; // is at level h+1, the null node is at level 0.
h = 0; // Set 'h' to the beginning of stack.
current = &root; // At first, the current node is the root node.
// start algorithm
for( ; list != NULL; list = list->next) // 'list' is the 'new node'
{
while(stack[h] == stack[h+1]+1) // While the tree-level ordering
{ h--; current = current->parent; } // is fine, climb up the tree.
stack[++h] = stack[h]+1; // Increment 'h' then set the tree-level of
stack[h+1] = 0; // the new node. Set null node's level to 0.
list->parent = current; // Insert the new node in the tree:
list->right = NULL; // set sub-right child to null,
list->left = current->right; // set old right child as sub-left child,
current->right = list; // set new right child to be the new node,
current = list; // set 'current' to be the new node,
if(list->left != NULL)
list->left->parent = list; // set new parent of sub-left child.
// Remove this 'else' part so to observe its important effect
// of ensuring that the tree is a 'complete' binary tree.
else if(leaves!=0)
{
leaves--; // the new node is a leave node, so count it
if(leaves==0) // if no more leaves then the null level will change
{
for(i=0; i<=h; i++) stack[i]--; // step all levels down, old leave
h--; current = current->parent; // level now becomes new null level
}
}
//print_tree(&root, 0);
}
// return the correct root of the tree
root.right->parent = NULL;
return root.right;
}
int main ()
{
int i, n=0;
Node *list=NULL;
Node *tree, *node;
while(1)
{
// get length 'n' of list
printf("Enter n (or 0 for next n): ");
scanf("%d", &i);
if(i<=0) n += 1;
else n = i;
// re-allocate memory
list = (Node*) realloc (list, n*sizeof(Node));
// construct linked-list
for(i=0; i < n-1; i++)
list[i].next = &list[i+1];
list[n-1].next = NULL;
// set list data (such that it is a sorted list)
for(i=1, node=list; node!=NULL; node = node->next, i++)
node->data = i;
// apply algorithm
tree = sorted_list_to_complete_binary_search_tree (list);
// print result
printf("--------------------------------------\r\n");
print_tree(tree, 0);
printf("--------------------------------------\r\n");
}
// free allocated memory...?
free(list);
return 0;
}
Links
- http://en.wikipedia.org/wiki/Binary_search_tree
- https://en.wikipedia.org/wiki/Tree_traversal
- https://ece.uwaterloo.ca/~cmoreno/ece250/4.05.PerfectBinaryTrees.pdf
- http://courses.cs.vt.edu/~cs3114/Fall09/wmcquain/Notes/T03a.BinaryTreeTheorems.pdf
- Algorithms - Expression parsing algorithm
See also