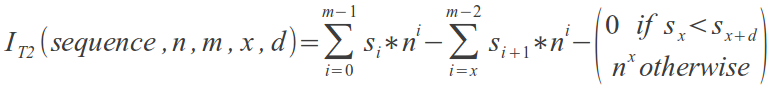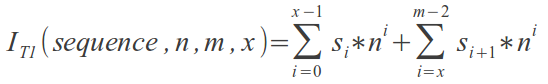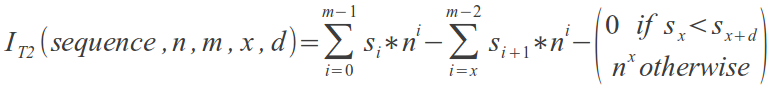Numbering sequences under xd restriction
Let S be the set of nm distinct sequences where every sequence represents a possible arrangement of n objects in m spaces. The n objects are labeled from 0 to n-1. For example let n=2 and m=3, then:
S = {
{ 0, 0, 0 },
{ 1, 0, 0 },
{ 0, 1, 0 },
{ 1, 1, 0 },
{ 0, 0, 1 },
{ 1, 0, 1 },
{ 0, 1, 1 },
{ 1, 1, 1 } }
This article presents the numbering of sequences in the set S and in two subsets of S: denoted T1 and T2. These subsets are obtained by restricting sequences in S based on two values x and d. Precisely, a sequence in S is also in T1 if and only if its xth and (x+d)th elements are equal, otherwise it is in T2. This has been described as the xd restriction.
Contents:
- Numbering sequences in the set S
- Numbering sequences in the set T1
- Numbering sequences in the set T2
Numbering sequences in the set S
The sequences in S can be numbered (or indexed) from 0 to nm-1. Let s be a particular sequence of the form {s0, s1, s2, ..., sm-2, sm-1}. slevel in this sequence is an integer between 0 and n-1 inclusive. It is found at a certain level (there are m levels from 0 to m-1). s is numbered (or indexed) by the indexing number I. So I ranges from 0 to nm-1.
Below is an example of numbered (or indexed) sequences in order, for the case of n=2 and m=3:
| index I | sequence S |
| 0 | 0 0 0 |
| 1 | 1 0 0 |
| 2 | 0 1 0 |
| 3 | 1 1 0 |
| 4 | 0 0 1 |
| 5 | 1 0 1 |
| 6 | 0 1 1 |
| 7 | 1 1 1 |
Essentially, this article deals with a new way of understanding the base-n numeral system. The sequence s is actually the equivalent of the indexing number I when this I is expressed in the base n. For example in base n=2, I=5 is represented as 101.
Given s and n, I is given by:
I = s0*n0 + s1*n1 + s2*n2 + ... + sm-2*nm-2 + sm-1*nm-1
Proof:
Prooving that the relationship between the set S, and the set of values of I under the equation above, is one-to-one.
First it should be noted that the largest computation of I with respect to the equation is for the sequence {n-1, n-1, n-1, ... m times}. In this case I evaluates to nm-1 (that is I = nm-1).
Now let any two sequences {sa,0 , sa,1 , sa,2 , ..., sa,m-2 , sa,m-1} and {sb,0 , sb,1 , sb,2 , ..., sb,m-2 , sb,m-1} be numbered Ia and Ib respectively, such that Ia=Ib. Then
Ia-Ib=0 => (sa,0 - sb,0)*n0 + (sa,1 - sb,1)*n1 + (sa,2 - sb,2)*n2 + ... + (sa,m-2 - sb,m-2)*nm-2 + (sa,m-1 - sb,m-1)*nm-1 = 0 .
It turns out that for the above equation to hold, every term must evaluate to zero. Consider the worst case scenario where the term (sa,m-1 - sb,m-1)*nm-1 becomes equal to (1)*nm-1, meanwhile the terms (sa,0 - sb,0)*n0, (sa,1 - sb,1)*n1, (sa,2 - sb,2)*n2 , ... and (sa,m-2 - sb,m-2)*nm-2 are all negative. The later all add up to form the most negative possible value of -(nm-1-1). In this worst case the value of I is equal to ( nm-1 - (nm-1-1) ) = 1 , which is different from 0.
Only the values in brackets can evaluate to zero. Consequently the only way for the equation to hold is that: sa,0=sb,0 , sa,1=sb,1 , sa,2=sb,2 , ... , sa,m-2=sb,m-2 and sa,m-1=sb,m-1. So the two sequences must be the same. It follows that the relationship is indeed one-to-one.
Given I and n, slevel in s is given by:
slevel = [ I / nlevel ] - [ I / nlevel+1 ]*n = [ (I mod nlevel+1) / nlevel ]
where [x] = floor(x) = largest integer smaller than or equal to x.
Proof:
Consider true that I = s0*n0 + s1*n1 + s2*n2 + ... + sm-2*nm-2 + sm-1*nm-1.
This represents computing the index I from the sequence s.
Now let y such that (substituting for slevel in the equation for I above):
y = ([ I / n0 ] - [ I / n1 ]*n)*n0 + ([ I / n1 ] - [ I / n2 ]*n)*n1 + ([ I / n2 ] - [ I / n3 ]*n)*n2 + ... + ([ I / nm-2 ] - [ I / nm-1 ]*n)*nm-2 + ([ I / nm-1 ] - [ I / nm ]*n)*nm-1
Simplifying the expression,
=> y = [ I / n0 ]*n0 - [ I / n1 ]*n1 + [ I / n1 ]*n1 - [ I / n2 ]*n2 + [ I / n2 ]*n2 - [ I / n3 ]*n3 + ... + [ I / nm-2 ]*nm-2 - [ I / nm-1 ]*nm-1 + [ I / nm-1 ]*nm-1 - [ I / nm ]*nm
After massive cancellation, only the first and last terms remain,
=> y = [ I / n0 ]*n0 - [ I / nm ]*nm
But I < nm,
=> y = I - 0
=> y = I
Since y=I, it follows that slevel = [ I / nlevel ] - [ I / nlevel+1 ]*n.
Numbering sequences in the set T1
The set T1 is made up of all sequences s that satisfy the xd restriction. This restriction is that the xth and (x+d)th elements must be equal, where d>0. There are a total of n(m-1) such sequences in T1. For n=m=3 the numbered sequences {s0, s1, s2} are as shown in the table below:
| S | x=0 d=1 | x=1 d=1 | x=0 d=2 |
|---|
| 0 - 0 0 0 | 0 - 0 0 0 | 0 - 0 0 0 | 0 - 0 0 0 |
| 1 - 1 0 0 | | 1 - 1 0 0 | |
| 2 - 2 0 0 | | 2 - 2 0 0 | |
| 3 - 0 1 0 | | | 1 - 0 1 0 |
| 4 - 1 1 0 | 1 - 1 1 0 | | |
| 5 - 2 1 0 | | | |
| 6 - 0 2 0 | | | 2 - 0 2 0 |
| 7 - 1 2 0 | | | |
| 8 - 2 2 0 | 2 - 2 2 0 | | |
| 9 - 0 0 1 | 3 - 0 0 1 | | |
| 10- 1 0 1 | | | 3 - 1 0 1 |
| 11- 2 0 1 | | | |
| 12- 0 1 1 | | 3 - 0 1 1 | |
| 13- 1 1 1 | 4 - 1 1 1 | 4 - 1 1 1 | 4 - 1 1 1 |
| 14- 2 1 1 | | 5 - 2 1 1 | |
| 15- 0 2 1 | | | |
| 16- 1 2 1 | | | 5 - 1 2 1 |
| 17- 2 2 1 | 5 - 2 2 1 | | |
| 18- 0 0 2 | 6 - 0 0 2 | | |
| 19- 1 0 2 | | | |
| 20- 2 0 2 | | | 6 - 2 0 2 |
| 21- 0 1 2 | | | |
| 22- 1 1 2 | 7 - 1 1 2 | | |
| 23- 2 1 2 | | | 7 - 2 1 2 |
| 24- 0 2 2 | | 6 - 0 2 2 | |
| 25- 1 2 2 | | 7 - 1 2 2 | |
| 26- 2 2 2 | 8 - 2 2 2 | 8 - 2 2 2 | 8 - 2 2 2 |
A sequence in T1 can be numbered (or indexed) by an integer I, where 0 <= I <= n(m-1)-1.
Given:
- n >= 1
- m >= 2
- x where 0 <= x <= m-2
- d = any (equation does not depend on d)
- s = {s0, s1, s2, ..., sm-2, sm-1} ,
the equation below finds the corresponding value of I for the given sequence in T1. That is for example:
- if s={1, 1, 0}, n=m=3, x=0 and d=any, then I=1
- if s={0, 1, 1}, n=m=3, x=1 and d=any, then I=3
- if s={2, 1, 2}, n=m=3, x=0 and d=any, then I=7
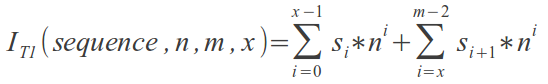
Numbering sequences in the set T2
The set T2 is made up of all sequences s that do not satisfy the xd restriction. This restriction is that the xth and (x+d)th elements must be equal, where d>0. There are a total of (n-1)n(m-1) such sequences in T2. For n=m=3 the numbered sequences {s0, s1, s2} are as shown in the table below:
| S | x=0 d=1 | x=1 d=1 | x=0 d=2 |
|---|
| 0 - 0 0 0 | | | |
| 1 - 1 0 0 | 0 - 1 0 0 | | 0 - 1 0 0 |
| 2 - 2 0 0 | 1 - 2 0 0 | | 1 - 2 0 0 |
| 3 - 0 1 0 | 2 - 0 1 0 | 0 - 0 1 0 | |
| 4 - 1 1 0 | | 1 - 1 1 0 | 2 - 1 1 0 |
| 5 - 2 1 0 | 3 - 2 1 0 | 2 - 2 1 0 | 3 - 2 1 0 |
| 6 - 0 2 0 | 4 - 0 2 0 | 3 - 0 2 0 | |
| 7 - 1 2 0 | 5 - 1 2 0 | 4 - 1 2 0 | 4 - 1 2 0 |
| 8 - 2 2 0 | | 5 - 2 2 0 | 5 - 2 2 0 |
| 9 - 0 0 1 | | 6 - 0 0 1 | 6 - 0 0 1 |
| 10- 1 0 1 | 6 - 1 0 1 | 7 - 1 0 1 | |
| 11- 2 0 1 | 7 - 2 0 1 | 8 - 2 0 1 | 7 - 2 0 1 |
| 12- 0 1 1 | 8 - 0 1 1 | | 8 - 0 1 1 |
| 13- 1 1 1 | | | |
| 14- 2 1 1 | 9 - 2 1 1 | | 9 - 2 1 1 |
| 15- 0 2 1 | 10- 0 2 1 | 9 - 0 2 1 | 10- 0 2 1 |
| 16- 1 2 1 | 11- 1 2 1 | 10- 1 2 1 | |
| 17- 2 2 1 | | 11- 2 2 1 | 11- 2 2 1 |
| 18- 0 0 2 | | 12- 0 0 2 | 12- 0 0 2 |
| 19- 1 0 2 | 12- 1 0 2 | 13- 1 0 2 | 13- 1 0 2 |
| 20- 2 0 2 | 13- 2 0 2 | 14- 2 0 2 | |
| 21- 0 1 2 | 14- 0 1 2 | 15- 0 1 2 | 14- 0 1 2 |
| 22- 1 1 2 | | 16- 1 1 2 | 15- 1 1 2 |
| 23- 2 1 2 | 15- 2 1 2 | 17- 2 1 2 | |
| 24- 0 2 2 | 16- 0 2 2 | | 16- 0 2 2 |
| 25- 1 2 2 | 17- 1 2 2 | | 17- 1 2 2 |
| 26- 2 2 2 | | | |
A sequence in T2 can be numbered (or indexed) by an integer I, where 0 <= I <= (n-1)n(m-1)-1.
Given:
- n >= 1
- m >= 2
- x where 0 <= x <= m-2
- d where 1 <= d <= m-1-x
- s = {s0, s1, s2, ..., sm-2, sm-1} ,
the equation below finds the corresponding value of I for the given sequence in T2. That is for example:
- if s={2, 0, 0}, n=m=3, x=0 and d=1, then I=1
- if s={1, 2, 0}, n=m=3, x=1 and d=1, then I=4
- if s={2, 1, 1}, n=m=3, x=0 and d=2, then I=9